标签： 杭州品茶工作室

The new drama "The Story of Chenghuan", which Yang Zi and Xu Kai collaborated on for the first time, has been eagerly awaited by fans and melon-eating netizens from both families. Xu Kai revealed in an interview a few days ago: The setting of the female lead of the drama, Mai Chenghuan, is a positive-energy silly white sweet. This low-EQ answer instantly aroused dissatisfaction among the female fans. Silly white sweet itself is not a word of praise, but it specifically refers to the female lead in idol dramas without a heart. But the promotion positioning of "The Story of Chenghuan" has always been an urban drama.

It can be seen from the filing information of "Chenghuan’s Story" that the drama is mainly based on the growth line of the eldest female protagonist Mai Chenghuan, focusing on the family, love and career of young people. It is fully attractive to the current film and television drama market. In addition, Yang Zi and Xu Kai are also famous for acting in ancient puppet dramas, so on the basis of attracting the original audience, fans will also be the main force of the drama’s ratings. Not long ago, the drama also appeared on CCTV’s 2024 film list, which shows that its warm and healing urban drama style is also loved by mainstream platforms.

I believe that with this drama, Yang Zi and Xu Kai can achieve more outstanding CVB results, and their performance in the same period will be even higher. Although Yang Zi and Xu Kai have not cooperated before, the atmosphere between the fans of the two sides is very harmonious, as if they are a win-win cooperation. However, from the moment Xu Kai said "Mai Chenghuan is a silly white sweet with positive energy", Yang Zi’s fans’ dissatisfaction with Xu Kai has skyrocketed. After all, most actors use more cautious words in interviews.

And Xu Kai gave an inappropriate evaluation of Yang Zi’s role that has not yet been broadcast. Either the play is sailing under false colors and pays too much attention to the development of the love line between the male and female protagonists; or it alludes to Yang Zi’s acting skills, and everything is like playing silly. In any case, Xu Kai’s low emotional intelligence answer in the interview is indeed worthy of other actors to learn from. However, before the show is broadcast, the large-scale tearing among actors and fans is likely to delay the show’s stardom process and affect the audience’s viewing experience.

So the fans on both sides tacitly did not make any big noise about this matter. Then again, the strong alliance between Yang Zi and Xu Kai this time can be said to be expected. As the boss of Xu Kai’s agency, Yu Zheng has always admired the actor Yang Zi’s ability to carry dramas and emotional explosive power, and told Xu Kai to cooperate with Yang Zi if he had the opportunity. Yu Zheng, who has always been picky about other actors, praised Yang Zi and encouraged his own company’s artists to choose to cooperate with Yang Zi as much as possible.

It can be seen that Yang Zi’s reputation in the industry is very good. Although Yu Zheng’s speaking style is very polite many times, the co-actors who can be recommended to their own artists with confidence must be very good. It seems that Yang Zi and Xu Kai’s cooperation this time should be fueled by Zheng. Xu Kai has starred in many film and television dramas since his debut, but his role in the drama is generally charming, and the performance and bonus of the starring drama are also very weak. This cooperation with Yang Zi, the queen of the explosion, should change this situation.

Yang Zi’s emotional and conflict dramas have always been great, always grabbing the audience’s attention in an instant. As early as when she was acting in ancient puppet dramas, Yang Zi’s acting skills were highly praised by the audience. However, Yang Zi’s portrayal of complex characters seems to be poor, and the previous broadcast of "Female Psychologist" is her transformation work. But Yang Zi does not seem to depict the arc of the character in the corner of Hutton, but all kinds of performances are floating on the surface, and the performance traces are too heavy, as if they are not in the same channel as other actors.

Perhaps it was because of Yang Zi’s poor performance in this drama that the final broadcast performance of this drama was very unsatisfactory. And during its broadcast, there was a scandal of "water injection", and Yang Zi was dubbed "Yang 800 million" overnight. Although Yang Zi’s performance in ancient puppet dramas was great, it seemed to have taken shape in modern dramas. Many audiences commented that Yang Zi acted like Qiu Yingying in everything. As an urban explosion drama produced by Noon Sunshine, Qiu Yingying’s role was relatively successful.

The character setting is a typical silly white and sweet, but Yang Zi’s unique acting style gives Qiu Yingying a different charm. Under Yang Zi’s shaping, Qiu Yingying’s character is not only unpleasant on the surface, but also deeper cute and simple. This may be the charm of a good actor. However, it may be because Qiu Yingying impresses the audience too deeply, so the audience will feel that Yang Zi’s acting skills for so many years have no progress and can only revolve within the comfort circle, and the ancient puppet drama circle is the ruling area of actor Yang Zi.

On the one hand, being trapped in ancient puppet dramas for a long time is indeed not conducive to the improvement of acting skills. On the other hand, there are already many young and beautiful 95 flowers and 00 flowers in ancient puppet dramas. If you don’t follow the footsteps of the same period of flowers, you will easily suffer in the later transformation. Fortunately, the production company of "Chenghuan Ji" is Huace Film and Television, and its popular urban dramas are deeply loved by audiences and have first-class star-making abilities. It is of great help to the development of actors.

For example, Song Weilong, Tan Songyun, and Yu Shuxin all became popular with the urban dramas produced by Huace Film and Television, so Yang Zi’s cooperation with Xu Kai in the film and television dramas produced by Huace should be a combination of strong and powerful situations. Yang Zi, who was once hindered in the process of transformation, must have been able to successfully reverse the reputation of his acting in the eyes of the audience with "Chenghuan". Although Xu Kai’s evaluation of Mai Chenghuan’s silly Baitian has connotations of Yang Zi’s acting skills and the suspicion of backstabbing the cast, Xu Kai’s performance is conducive to increasing the audience of the drama.

Although there was no shortage of film and television resources after Xu Kai’s debut, the evaluation of the female lead of "Chenghuan" also exposed Xu Kai’s illiteracy in a certain way. Perhaps because it was not necessary to have a high degree to be an actor, many actors in the entertainment industry interviewed very unnourished, and even said bumps and bumps when receiving the award speech. There are too few people who can say something and understand the characters thoroughly. Xu Kai’s use of silly Baitian to describe the female lead would make the two a little embarrassed when they combined in the later stage of the promotional drama.

After all, Yang Zi had been evaluated by the audience for a long time as "playing everything is like playing Qiu Yingying". He must be holding his breath in his heart, wanting to use the hit of "Chenghuan" to change the audience’s impression. Now that Xu Kai’s evaluation of Silly Baitian is out, Yang Zi’s impression of him is bound to be greatly discounted. However, the reason why Xu Kai used "Silly Baitian with positive energy" to describe Mai Chenghuan may not be because of low emotional intelligence, but because the adjective he could think of at that moment was Silly Baitian.

Writing | Zuo Chao Qian Jiaming

In March 2016, DeepMind, a Google-owned artificial intelligence (AI) company, defeated Go world champion Lee Sedol 4:1 with its AlphaGo artificial intelligence system, triggering a new wave of artificial intelligence – deep learning technology. Since then, people have witnessed the rapid rise and wide application of deep learning technology – it has solved many problems and challenges in computer vision, computational imaging, and computer-aided diagnostics with unprecedented performance. At the same time, Google, Facebook, Microsoft, Apple, and Amazon, the five tech giants without exception, are investing more and more resources to seize the artificial intelligence market, and even transforming into artificial intelligence-driven companies as a whole. They have begun to "ignite" the "art" of data mining and developed easy-to-use open-source deep learning frameworks. These deep learning frameworks enable us to use pre-built and optimized component sets to build complex, large-scale deep learning models in a clearer, concise, and user-friendly way without having to delve into the details of the underlying algorithms. Domestic "BAT" also regards deep learning technology as a key strategic direction, and actively deploys the field of artificial intelligence with its own advantages. Deep learning has rapidly left the halls of academia and is beginning to reshape industry.

Optical metrology, on the other hand, is a type of measurement science and technology that uses optical signals as the standard/information carrier. It is an ancient discipline, because the development of physics has been driven by optical metrology from the very beginning. But in turn, optical metrology has also undergone major changes with the invention of lasers, charge-coupled devices (CCDs), and computers. It has now developed into a broad interdisciplinary field and is closely related to disciplines such as photometry, optical engineering, computer vision, and computational imaging. Given the great success of deep learning in these related fields, researchers in optical metrology cannot suppress their curiosity and have begun to actively participate in this rapidly developing and emerging field. Unlike traditional methods based on "physics a priori", "data-driven" deep learning technology offers new possibilities for solving many challenging problems in the field of optical metrology, and shows great application potential.

In this context, in March 202,Nanjing University of Science and TechnologywithNanyang Technological University, SingaporeThe research team published in the top international optical journal "Lighting: Science & Applications"A joint statement entitled"Deep learning in optical metrology: a review"The first author of the review article is Nanjing University of Science and TechnologyZuo ChaoProfessor, PhD student at Nanjing University of Science and TechnologyQian JiamingCo-first author, Nanjing University of Science and TechnologyZuo Chao,Chen QianProfessor, Nanyang Technological University, SingaporeChandler SpearProfessor is the co-corresponding author of the paper, and Nanjing University of Science and Technology is the first unit of the paper.

This paper systematically summarizes the classical techniques and image processing algorithms in optical metrology, briefly describes the development history, network structure and technical advantages of deep learning, and comprehensively reviews its specific applications in various optical metrology tasks (such as fringe denoising, phase demodulation and phase unwrapping). By comparing the similarities and differences in principle and thought between deep learning methods and traditional image processing algorithms, the unique advantages of deep learning in solving "problem reconstruction" and "actual performance" in various optical metrology tasks are demonstrated. Finally, the paper points out the challenges faced by deep learning technology in the field of optical metrology, and looks forward to its potential future development direction.

Traditional optical metrology

Image generation model and image processing algorithm

Optical metrology technology cleverly uses the basic properties of light (such as amplitude, phase, wavelength, direction, frequency, speed, polarization and coherence, etc.) as the information carrier of the measured object to realize the acquisition of various characteristic data of the measured object (such as distance, displacement, size, morphology, roughness, strain and stress, etc.). Optical metrology has been increasingly widely used in CAD /CAE, reverse engineering, online detection, quality control, medical diagnosis, cultural relics protection, human-interaction machine and other fields due to its advantages of non-contact, high speed, high sensitivity, high resolution and high accuracy.In optical metrology, the most common information carriers are "streaks" and "speckles."For example, the images processed by most interferometry methods (classical interference, photoelasticity, digital speckle, digital holography, etc.) are interference fringes formed by the coherent superposition of object light and reference light, and the measured physical quantity is modulated in the phase information of the interference fringes. In addition, the fringe pattern can also be generated in a non-interferometric way, such as fringe projection profilometry (FPP) directly projecting the fringe pattern of structured light to the surface of the measured object to measure the three-dimensional surface shape of the object. In digital image correlation (DIC), the captured image is the speckle pattern before and after the deformation of the sample surface, from which the total field displacement and deformation distribution of the measured object can be obtained. Combining DIC with stereo vision or photogrammetry, the depth information of the measured scene can also be obtained based on multi-view speckle images. Figure 1 summarizes the image generation process of these techniques and their corresponding mathematical models.

Figure 1 The image generation process and corresponding mathematical model in traditional optical metrology technology

Traditional optical metrology is inseparable from image processing technologyImage processing of fringe/speckleIt can be understood as a process of inverting the required physical quantity to be measured from the captured original intensity image. Usually, this process is not "Instead, it consists of three logically hierarchical image processing steps – pre-processing, analysis, and post-processing.Each step involves a series of image processing algorithms, which are layered on top of each other to form a "pipeline" structure [Figure 2], where each algorithm corresponds to a "map"Operation, which converts the matrix input of an image/similar image into the output of the corresponding dimension (or resampling)."

(1) PretreatmentImage preprocessing improves image quality by suppressing or minimizing unnecessary interference signals (such as noise, aliasing, distortion, etc.). Representative image preprocessing algorithms in optical metrology include image denoising, image enhancement, color channel separation, and image registration and correction.

(2) Analysis: Image analysis is the core step of image processing algorithms, which is used to extract important information carriers related to the physical quantities to be measured from the input image. In phase measurement technology, the main task of image analysis is to reconstruct phase information from fringe images. The basic algorithms include phase demodulation and phase unfolding. For stereo matching technology, image analysis refers to determining the displacement vector between points corresponding to the speckle image (the speckle pattern before and after the deformation of the sample surface/the multi-view speckle image), which generally includes two steps of subset matching and sub-pixel optimization.

(3) Post-processing:The purpose of image post-processing is to further optimize the measured phase data or speckle displacement fields and eventually convert them into physical quantities to be measured. Common post-processing algorithms in optical metrology include noise removal, error compensation, digital refocus, and parameter conversion. Figure 3 provides an overview of the image processing hierarchy of optical metrology and various image processing algorithms distributed in different layers.

A typical image processing process for optical metrology (e.g. fringe projection profiling) can be divided into three main steps: preprocessing (e.g. denoising, image enhancement), analysis (e.g. phase demodulation, phase unwrapping), and post-processing (e.g. phase-depth mapping).

Figure 3 Overview of the optical metrology image processing hierarchy and various image processing algorithms distributed in different layers

Deep learning technology

Principle, development and convolutional neural networks

Deep learning is an important branch in the field of machine learning. It builds neural structures that simulate the information processing of the human brainArtificial neural networks (ANN), enabling machines to perform bottom-up feature extraction from large amounts of historical data, thus enabling intelligent decision-making on future/unknown samples. ANN originated from a simplified mathematical model of biological nerve cells established by McCulloch and Pitts in 1943 2 ?? [Fig. 4a]. In 1958, Rosenblatt et al 2 ??, inspired by the biological nerve cell model, first proposed a machine that could simulate human perceptual abilities – a single-layer perceptron. As shown in Fig. 4b, a single-layer perceptron consists of a single nerve cell. The nerve cell maps the input to the output through a non-linear activation function with bias (b) and weight (w) as parameters. The proposal of perceptrons has aroused the interest of a large number of researchers in ANNs, which is a milestone in the development of neural networks. However, the limitation that single-layer perceptrons can only handle linear classification problems has caused the development of neural networks to stagnate for nearly 20 years. In the 1980s, the proposal of backpropagation (BP) algorithm made it possible to train multi-layer neural networks efficiently. It continuously adjusts the weights between nerve cells based on the chain rule to reduce the output error of multi-layer networks, effectively solving the problem of nonlinear classification and learning, triggering a boom in "shallow learning" 2 2. In 1989, LeCun et al. 2 3 proposed the idea of convolutional neural networks (CNNs) inspired by the structure of mammalian visual cortex, which laid the foundation for deep learning for modern computer vision and image processing. Subsequently, as the number of layers of neural networks increased, the problem of layer disappearance/explosion of BP algorithm became increasingly prominent, which caused the development of ANN to stagnate in the mid-1990s. In 2006, Hinton et al. proposed a deep belief network (DBN) training method to deal with the problem of layer disappearance; at the same time, with the development of computer hardware performance, GPU acceleration technology, and the emergence of a large number of labeled datasets, neural networks entered the third development climax, from the "shallow learning" stage to the "deep learning" stage. In 2012, AlexNet based on CNN architecture won the ImageNet image recognition competition in one fell swoop, making CNN one of the mainstream frameworks for deep learning after more than 20 years of silence. At the same time, some new deep learning network architectures and training methods (such as ReLU 2 and Dropout 2)It was proposed to further solve the problem of layer disappearance, which promoted the explosive growth of deep learning. In 2016, AlphaGo, an artificial intelligence system developed by Google’s AI company DeepMind, defeated Lee Sedol, the world champion of Go, which aroused widespread attention to deep learning technology among all mankind 2. Figure 4 shows the development process of artificial neural networks and deep learning technologies and the structural diagram of typical neural networks.

Figure 4 The development process of deep learning and artificial neural networks and the structural diagram of typical neural networks

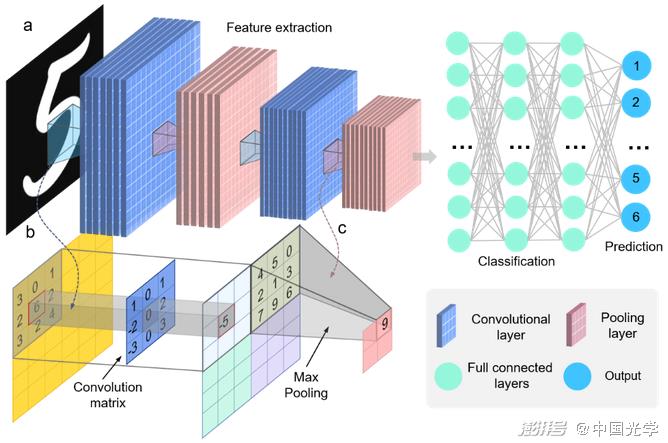
Figure 5 Typical CNN structure for image classification tasks　　

A) A typical CNN consists of an input layer, a convolutional layer, a fully connected layer, and an output layer b) a convolutional operation c) a pooling operation

The single-layer perceptron described above is the simplest ANN structure and consists of only a single nerve cell [Fig. 4b]. Deep neural networks (DNNs) are formed by connecting multiple layers of nerve cells to each other, with nerve cells between adjacent layers typically stacked in a fully connected form [Fig. 4g]. During network training, the nerve cell multiplies the corresponding input by a weight coefficient and adds it to the bias value, outputting it to the next layer through a non-linear activation function, while network losses are computed and backpropagated to update network parameters. Unlike conventional fully connected layers, CNNs use convolutional layers to perform feature extraction on the input data 2 [Fig. 5a]. In each layer, the input image is convoluted with a set of convolutional filters and added biases to generate a new output image [Fig. 5b]. Pooling layers in CNNs take advantage of the local correlation principle of the image to subsample the image, reducing the amount of data processing while preserving useful information [Fig. 5c]. These features make CNNs widely used in tasks of computer vision, such as object detection and motion tracking. Traditional CNN architectures are mostly oriented towards "classification" tasks, discarding spatial information at the output and producing an output in the form of a "vector". However, for image processing tasks in optical metrology techniques, neural networks must be able to produce an output with the same (or even higher) full resolution as the input. For this purpose, a fully convolutional network architecture without a fully connected layer should be used. Such a network architecture accepts input of any size, is trained with regression loss, and produces pixel-level matrix output. Networks with such characteristics are called "fully convolutional network architectures" CNNs, and their network architectures mainly include the following three categories:

(1) SRCNN:Dong et al. 3 2 skip the pooling layer in the traditional CNN structure and use a simple stacking of several convolutional layers to preserve the input dimension at the output [Fig. 6a]. SRCNN constructed using this idea has become one of the mainstream network frameworks for image super-resolution tasks.

(2) FCN:A fully convolutional network (FCN) is a network framework for semantic segmentation tasks proposed by Long et al. As shown in Figure 6b, FCN uses the convolutional layer of a traditional CNN [Fig. 5] as the network coding module and replaces the fully connected layer with a deconvolutional layer as the decoding module. The deconvolutional layer is able to upsample the feature map of the last convolutional layer so that it recovers to an output of the same size as the input image. In addition, FCN combines coarse high-level features with detailed low-level features through a skip structure, allowing the network to better recover detailed information while preserving pixel-level output.

(3) U-Net:Ronneberger et al. made improvements to FCN and proposed U-Net network 3. As shown in Figure 6c, the basic structure of U-Net includes a compressed path and an extended path. The compressed path acts as the encoder of the network, using four convolutional blocks (each convolutional block is composed of three convolutional layers and a pooling layer) to downsample the input image and obtain the compressed feature representation; the extended path acts as the network decoder using the upsampling method of transposed convolution to output the prediction result of the same size as the input. U-Net uses jump connection to perform feature fusion on the compressed path and the extended path, so that the network can freely choose between shallow features and deep features, which is more advantageous for semantic segmentation tasks.

The above-mentioned fully convolutional network structure CNN can convert input images of any size into pixel-level matrix output, which is completely consistent with the input and output characteristics of the "mapping" operation corresponding to the image processing algorithm in the optical metrology task, so it can be very convenient to "deep learning replacement" for traditional image processing tasks, which laid the foundation for the rapid rise of deep learning in the field of optical metrology.

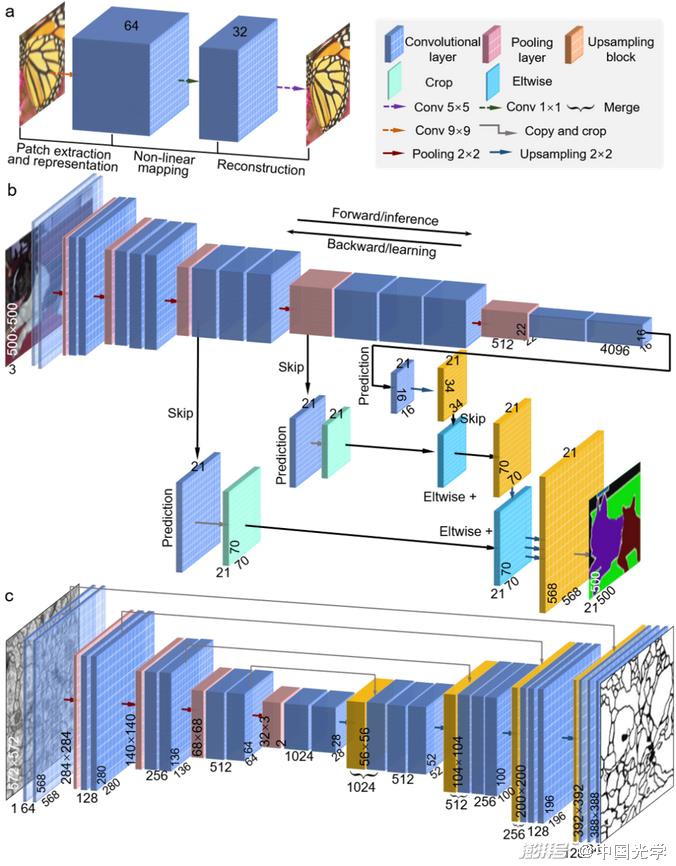
Fig.6 Three representative fully convolutional network architectures of CNNs capable of generating pixel-level image output for image processing tasks

A) SRCNN b) FCN c) U-Net.

Optical metrology in deep learning

Changes in thinking and methodology

In optical metrology, the mapping between the original fringe/speckle image and the measured physical quantity can be described as a combination of forward physical model and measurement noise from parameter space to image space, which can explain the generation process of almost all original images in optical metrology. However, extracting the physical quantity to be measured from the original image is a typical "inverse problem". Solving such inverse problems faces many challenges, such as: unknown or imprecise forward physical model, error accumulation and local optimal solution, and pathology of inverse problems. In the field of computer vision and computational imaging, the classic method for solving inverse problems is to define the solution space by introducing the prior of the measured object as a regularization means to make it well-conditioned [Figure 7]. In the field of optical metrology, the idea of solving the inverse problem is quite different. The fundamental reason is that optical metrology is usually carried out in a "highly controllable" environment, so it is more inclined to "actively adjust" the image acquisition process through a series of "active strategies", such as lighting modulation, object regulation, multiple exposures, etc., which can reshape the original "sick inverse problem" into a "well-conditioned and sufficiently stable regression problem". For example, demodulating the absolute phase from a single fringe image: the inverse problem is ill-conditioned due to the lack of sufficient information in the forward physical model to solve the corresponding inverse problem uniquely and stably. For researchers in optical metrology, the solution to this problem is very simple: we can make multiple measurements, and by acquiring additional multi-frequency phase-shifted fringe images, the absolute phase acquisition problem evolves into a good-state regression problem. We can easily recover the absolute phase information of the measured object from these fringe images by multi-step phase-shifting and time-phase unwrapping [Figure 8].

Figure 7 In computer vision (e.g. image deblurring), the inverse problem is ill-conditioned because the forward physical model mapped from the parameter space to the image space is not ideal. A typical solution is to reformulate the original ill-conditioned problem as a well-conditioned optimization problem by adding some prior assumptions (smoothing) that aid regularization

Fig. 8 Optical metrology transforms a ill-conditioned inverse problem into a well-conditioned regression problem by actively controlling the image acquisition process. For example, in fringe projection profilometry, by acquiring additional phase-shifted fringe images of different frequencies, the absolute phase can be easily obtained by multi-frequency phase-shift method and temporal phase expansion method

However, when we step out of the laboratory and into the complex environment of the real world, the situation can be very different. The above active strategies often impose strict restrictions on the measurement conditions and the object being measured, such as:Stable measurement system, minimal environmental disturbance, static rigid objects, etcHowever, for many challenging applications, such as harsh operating environments and fast-moving objects, the above active strategy may become a "Luxury"Even impractical requirements. In this case, traditional optical metrology methods will face serious physical and technical limitations, such as limited data volume and uncertainty of forward models.How to extract high-precision absolute (unambiguous) phase information from minimal (preferably single-frame) fringe patterns remains one of the most challenging problems in optical metrology today.Therefore, we look forward to innovations and breakthroughs in the principles and methods of optical metrology, which are of great significance for its future development.

As a "data-driven" technology that has emerged in recent years, deep learning has received more and more attention in the field of optical metrology and has achieved fruitful results in recent years. Different from traditional physical model-driven methods,The deep learning method creates a set of training datasets composed of real target parameters and corresponding original measurement data, establishes their mapping relationships using ANN, and learns network parameters from the training dataset to solve the inverse problem in optical metrology[Figure 9]. Compared to traditional optical metrology techniques, deep learning moves active strategies from the actual measurement phase to the network training phase, gaining three unprecedented advantages:

1) From "model-driven" to "data-driven"Deep learning overturns the traditional "physical model-driven" approach and opens up a new paradigm based on "data-driven". Reconstruction algorithms (inverse mappings) can learn from experimental data without prior knowledge of physical models. If the training dataset is collected based on active strategies in a real experimental environment (including measurement systems, sample types, measurement environments, etc.), and the amount of data is sufficient (diversity), then the trained model should be able to reflect the real situation more accurately and comprehensively, so it usually produces more accurate reconstruction results than traditional physical model-based methods.

(2) From "divide and conquer" to "end-to-end learning":Deep learning allows for "end-to-end" learning of structures in which neural networks can learn a direct mapping relationship between raw image data and the desired sample parameters in one step, as shown in Figure 10, compared to traditional optical metrology methods of independently solving sequences of tasks. The "end-to-end" learning method has the advantage of synergy compared to "step-by-step divide-and-conquer" schemes: it is able to share information (features) between parts of the network performing different tasks, contributing to better overall performance compared to solving each task independently.

(3) From "solving linear inverse problems" to "directly learning pseudo-inverse maps": Deep learning uses complex neural networks and nonlinear activation functions to extract high-dimensional features of sample data, and directly learns a nonlinear pseudo-inverse mapping model ("reconstruction algorithm") that can fully describe the entire measurement process (from the original image to the physical quantity to be measured). For regularization functions or specified priors than traditional methods, the prior information learned by deep learning is statistically tailored to real experimental data, which in principle provides stronger and more reasonable regularization for solving inverse problems. Therefore, it bypasses the obstacles of solving nonlinear ill-conditioned inverse problems and can directly establish the pseudo-inverse mapping relationship between the input and the desired output.

Fig. 9 Optical metrology based on deep learning　　

A) In deep learning-based optical metrology, the mapping of image space to parameter space is learned from a dataset by building a deep neural network b) The process of obtaining a training dataset through experimentation or simulation.

Figure 10 Comparison of deep learning and traditional algorithms in the field of fringe projection

A) The basic principle of fringe projection profiling is 3D reconstruction based on optical triangulation (left). Its steps generally include fringe projection, phase recovery, phase unwrapping, and phase-height mapping b) Deep learning-based fringe projection profiling is driven by a large amount of training data, and the trained network model can directly predict the encoded depth information from a single frame of fringes

Application of deep learning in optical metrology

A complete revolution in image processing algorithms

Due to the above advantages, deep learning has received more and more attention in optical metrology, bringing a subversive change to the concept of optical metrology technology. Deep learning abandons the strict reliance on traditional "forward physical models" and "reverse reconstruction algorithms", and reshapes the basic tasks of digital image processing in almost all optical metrology technologies in a "sample data-driven" way. Breaking the functional/performance boundaries of traditional optical metrology technologies, mining more essential information of scenes from very little raw image data, significantly improving information acquisition capabilities, and opening a new door for optical metrology technology.Figure 11 reviews typical research efforts using deep learning techniques in the field of optical metrology. Below are specific application cases of deep learning in optical metrology according to the image processing level of traditional optical metrology techniques.

Figure 11 Deep learning in optical metrology: Since deep learning has brought significant conceptual changes to optical metrology, the implementation of almost all tasks in optical metrology has been revolutionized by deep learning

(1) Image preprocessing:Early work on applying deep learning to optical metrology focused on image preprocessing tasks such as image denoising and image enhancement. Yan et al. constructed a CNN composed of 20 convolutional layers to achieve fringe image denoising [Fig. 12a]. Since noise-free ideal fringe images are difficult to obtain experimentally, they simulated a large number of fringe images with Gaussian noise added (network input) and corresponding noise-free data (true value) as training datasets for neural networks. Figures 12d-12e show the denoising results of traditional denoising methods – windowed Fourier transform (WFT 3) and deep learning methods. It can be seen from the results that the deep learning-based method overcomes the edge artifacts of traditional WFT and exhibits better denoising performance. Shi et al. proposed a deep learning-based method for fringe information enhancement [Fig. 13a]. They used the fringe images captured in real scenes and the corresponding quality-enhanced images (acquired by subtracting two fringe images with a phase shift of π) as a dataset to train neural networks to achieve a direct mapping between the fringe images to the quality-enhanced fringe information. Fig. 13b-Fig. 13d shows the results of the 3D reconstruction of the moving hand by the traditional Fourier transform (FT) 3 and deep learning methods. From this, it can be seen that the deep learning method is significantly better than the traditional method in imaging quality.

Figure 12 The denoising method of fringe image based on deep learning and the denoising results of different methods.

A) The process of fringe denoising using depth learning: the fringe image with noise is used as the input of neural networks to directly predict the denoised image b) the input noise image c) the true phase distribution d) the denoising result of deep learning e) the denoising result of WFT 3

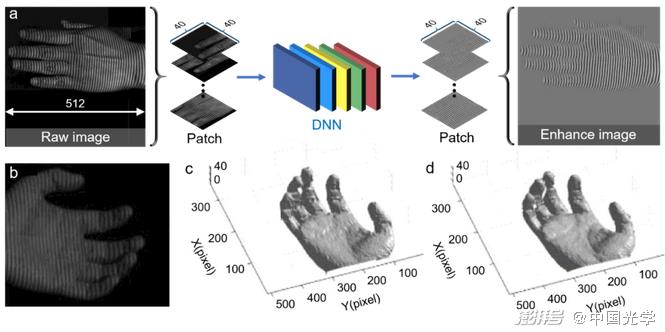
Fig. 13 Fringe information enhancement method based on deep learning and 3D reconstruction results under different methods.

A) using depth learning for fringe information addition process: the original fringe image and the acquired quality enhancement image are used to train DNN to learn the mapping between the input fringe image and the output quality enhancement fringe information b) input fringe image c) conventional FT method 38 3D reconstruction results d) 3D reconstruction results of deep learning method

(2) Image analysis:Image analysis is the most core image processing link in optical metrology technology, so most deep learning techniques applied to optical metrology are for processing tasks related to image analysis. For phase measurement technology, deep learning has been widely explored in phase demodulation and phase unwrapping. Zuo et al. applied deep learning technology to fringe analysis for the first time, and effectively improved the three-dimensional measurement accuracy of FPP. The idea of this method is to use only one fringe image as input, and use CNN to simulate the phase demodulation process of the traditional phase shift method. As shown in Figure 14a, two convolutional neural networks (CNN1 and CNN 2) are constructed, where CNN1 is responsible for processing the fringe image from the input (IExtract background information (ACNN 2 then uses the extracted background image and the sinusoidal portion of the desired phase of the original input image generation.M) and the cosine part (D); Finally, the output sine-cosine result is substituted into the arctangent function to calculate the final phase distribution. Compared with the traditional single-frame phase demodulation methods (FT 3 and WFT 3), the deep learning-based method can extract phase information more accurately, especially for the surface of objects with rich details, and the phase accuracy can be improved by more than 50%. Only one input fringe image is used, but the overall measurement effect is close to the 12-step phase shift method [Fig. 14b]. This technology has been successfully applied to high-speed 3D imaging, achieving high-precision 3D surface shape measurement up to 20000Hz [Fig. 14c]. Zuo et al. further generalized deep learning from phase demodulation to phase unwrapping, and proposed a deep learning-based geometric phase unwrapping method for single-frame 3D topography measurement. As shown in Figure 15a, the stereo fringe image pairs and reference plane information captured under the multi-view geometric system are fed into the CNN to determine the fringe order. Figures 15b-15e show the 3D reconstruction results obtained by the traditional geometric phase unwrapping method and the deep learning method. These results show that the deep learning-based method can achieve phase unwrapping of dense fringe images in a larger measurement volume and more robustly under the premise of projecting only a single frame of fringe images.

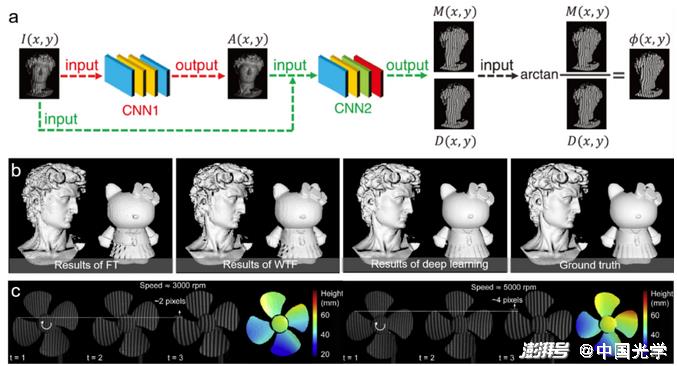
Fig. 14 Fringe analysis method based on deep learning and three-dimensional reconstruction results under different methods 3 a) Fringe analysis method flow based on deep learning: First, the background image A is predicted from the single frame fringe image I by CNN1; then CNN2 is used to realize the fringe pattern I, The mapping between the background image A and the sinusoidal part M and the cosine part D that generate the desired phase; finally, the phase information can be wrapped with high accuracy through the tangent function b) Comparison of three-dimensional reconstruction of different phase demodulation methods (FT 3, WFT 3, deep learning-based method and 12-step phase shift method 3 3) c) Deep reconstruction results of a high-speed rotating table fan using depth learning method

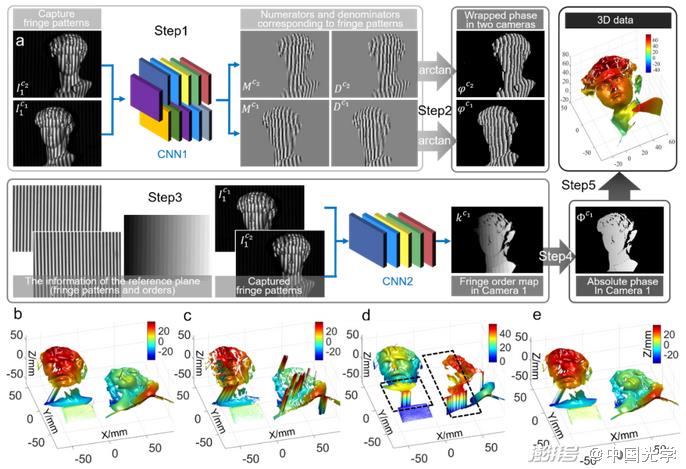
Fig. 15 Geometric phase unwrapping method based on deep learning and 3D reconstruction results under different methods < unk > a) Flow of geometric phase unwrapping method assisted by deep learning: CNN1 predicts the wrapping phase information from the stereo fringe image pair, CNN2 predicts the fringe order from the stereo fringe image pair and reference information. The absolute phase can be recovered by the predicted wrapping phase and fringe order, and then 3D reconstruction is performed b) 3D reconstruction results obtained by combining phase shift method, three-camera geometric phase expansion technique, and adaptive depth constraint method, c) 3D reconstruction results obtained by combining phase shift method, two-camera geometric phase expansion technique, d) 3D reconstruction results obtained by geometric constraint method based on reference surface, e) 3D reconstruction results obtained by deep learning method

Deep learning is also widely used for stereo matching and achieves better performance than traditional subset matching and sub-pixel optimization methods. Zbontar and LeCun ?? propose a deep learning method for stereo image disparity estimation [Fig. 16]. They constructed a Siamese-type CNN to solve the matching cost calculation problem by learning similarity metrics from two image blocks. The output of the CNN is used to initialize the stereo matching cost, and then to achieve disparity map estimation by refining the initial cost through cross-based cost aggregation and semi-global matching. Fig. 16d-Fig. 16h are disparity images obtained by traditional Census transformation and deep learning methods. From this, it can be seen that the deep learning-based method achieves lower error rates and better prediction results. Pang et al. propose a cascaded CNN architecture for sub-pixel matching. As shown in Figure 17a, the initial disparity estimation is first predicted from the input stereo image pair by DispFulNet with upsampling module, and then the multi-scale residual signal is generated by the hourglass-structured DispResNet, which synthesizes the output of the two networks and finally obtains the disparity map with sub-pixel accuracy. Figures 17d-17g show the disparity map and error distribution predicted by DispfulNet and DispResNet. It can be seen from the experimental results that the quality of the disparity map has been significantly improved after the optimization of DispResNet in the second stage.

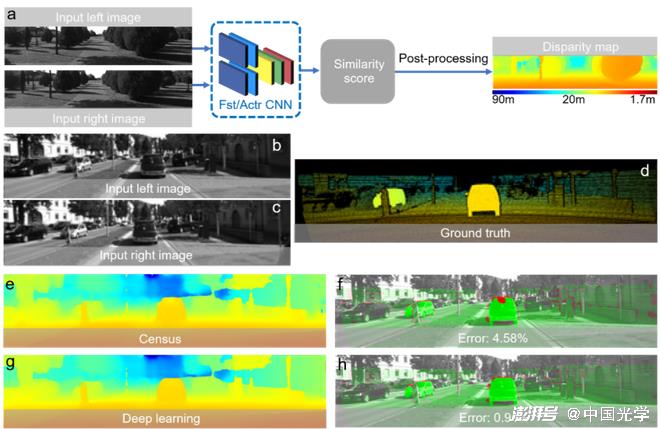
Figure 16 The disparity estimation results of the subset matching method based on deep learning and the disparity estimation results of different methods ?? a) The algorithm flow of disparity map estimation using depth learning: Siamese CNN is constructed to learn similarity metrics from two image blocks to solve the matching cost calculation problem, and finally realizes the disparity estimation through a series of post-processing b-c) The input stereo image d) true value e, g) Census and the disparity estimation results obtained by CNN

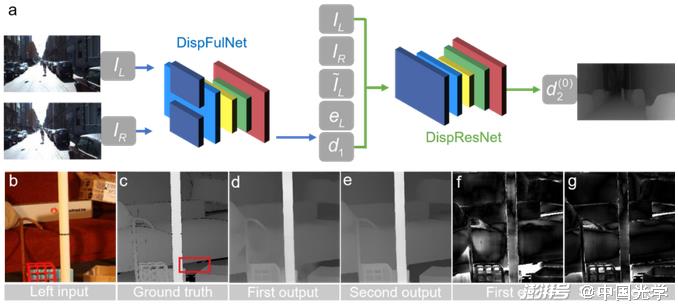
Figure 17 a) Sub-pixel matching method based on deep learning: First, the initial disparity estimation is predicted from the input stereo image pair through DispFulNet, and then the multi-scale residual signal is generated through the hourglass structure DispResNet, and the final output of the two networks is obtained. The disparity map with sub-pixel accuracy b) the left viewing angle of the input stereo image c) true value d-g) the disparity map and error distribution predicted by DispfulNet and DispResNet

(3) Post-processing: Deep learning also plays an important role in the post-processing phase of optical metrology (phase denoising, error compensation, digital refocus, phase-height mapping, etc.). As shown in Figure 18a, Montresor et al. input the sine and cosine components of the noise phase image into the CNN to predict the noise-removed high-quality phase image, and the predicted phase is fed back to the CNN for iterative refining to achieve better denoising effect. Figures 18b-18e show the phase denoising results of the traditional WFT 3 method and the deep learning method. Experimental results show that the CNN can achieve lower denoising performance than the WFT peak-valley phase error.

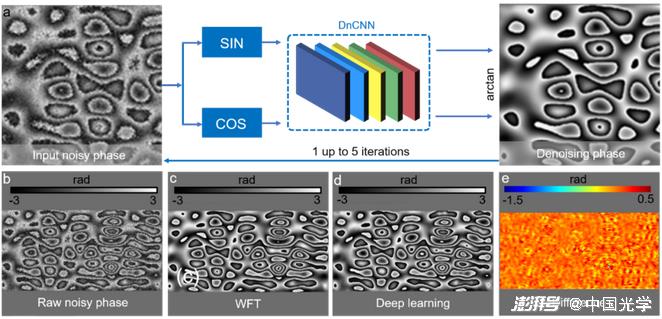
Figure 18 Phase denoising method based on deep learning and phase denoising results of different methods a) The process of phase denoising using depth learning: the sine and cosine components of the noise phase image are input to the CNN to predict the high-quality phase image with noise removal, and the predicted phase is fed back to the CNN again for iterative refining to achieve better denoising effect b) input noise phase image c) denoising result of WTF 3 d) denoising result of deep learning e) Comparison of WTF and deep learning method denoising results

Li et al. proposed a phase-height mapping method for fringe projection profilometry based on shallow BP neural networks. As shown in Figure 19a, the camera image coordinates and the corresponding projector image horizontal coordinates are used as network inputs to predict the three-dimensional information of the measured object. To obtain training data, the dot calibration plate is fixed on a high-precision displacement table and stripe images of the calibration plate are captured at different depth positions. By extracting the sub-pixel centers of the calibration plate dots, and using the absolute phase, the matching points of the camera and projector images corresponding to each marker center are calculated. Figures 19c and 19d show the error distribution of the three-dimensional surface shape results of the stepped standard parts obtained by the traditional phase height conversion method < unk > < unk > and the neural networks method. The results show that the neural networks-based method can learn more accurate phase height models from a large amount of data.

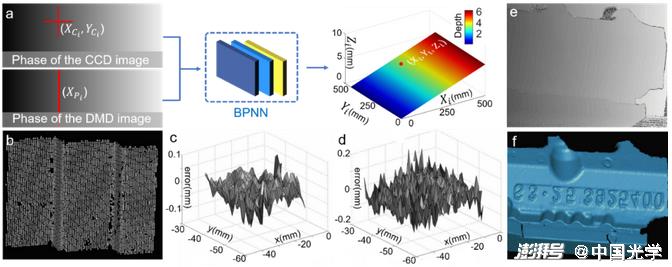
Fig. 19 a) Learning-based phase-depth mapping method: camera image coordinates and the horizontal coordinates of the corresponding projector image are used as network inputs to predict the three-dimensional information of the measured object b) The three-dimensional results of the step-shaped standard obtained by the learning-based method c, d) Error distribution of the three-dimensional surface shape results of the step-shaped standard obtained by the traditional phase height conversion method ?? and neural networks method e, f) Input phase images and output three-dimensional information of complex workpieces

Challenges and opportunities of deep learning in optical metrology

At present, deep learning has gradually "penetrated" into the discipline of computational imaging and optical measurement, and has shown amazing performance and strong application potential in fringe analysis, phase recovery, phase unfolding, etc. However, deep learning still faces many challenges in the field of optical metrology:

(1) As a data-driven technology, the performance of deep learning network output largely depends on a large number of labeled training data. The data collection process of most optical metrology experiments is complicated and time-consuming, and often the ideal true value cannot be obtained accurately and reliably after data collection [Figure 20].

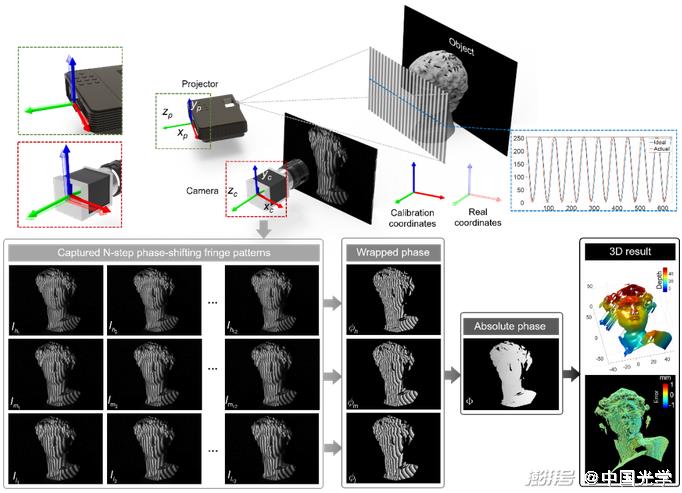
Fig. 20 The challenge of deep learning in optical metrology – the high cost of acquiring and labeling training data. Taking fringe projection profilometry as an example, the multi-frequency time phase unwrapping method is used to obtain high-quality training data at the cost of projecting a large number of fringe images. However, in practice, hardware errors, ambient light interference, calibration errors and other factors make it difficult to obtain the ideal true value through traditional algorithms

(2) So far, there is still no theory that clearly explains what structure of neural networks is most suitable for specific imaging needs [Figure 21]?

(3) The success of deep learning usually depends on the "common" features learned and extracted from the training examples as prior information. Therefore, when artificial neural networks are faced with "rare examples", it is very easy to give a wrong prediction without realizing it.

(4) Unlike the traditional "transparent" deduction process based on physical model methods, most current deep learning-based decision-making processes are generally regarded as "black boxes" driven by training data. In optical metrology, interpretability is often crucial, as it ensures traceability of errors.

(5) Since information is not "created out of nothing", the results obtained by deep learning cannot always be accurate and reliable. This is often fatal for many application fields of optical measurement, such as reverse engineering, automatic control, defect detection, etc. In these cases, the accuracy, reliability, repeatability and traceability of the measurement results are the primary considerations.

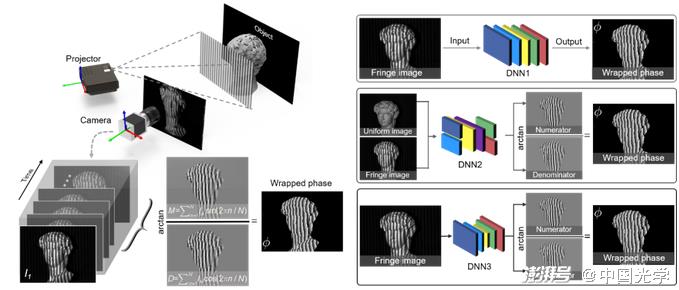
Figure 21 The challenge of deep learning in optical metrology – empiricism in model design and algorithm selection. Taking phase extraction in fringe projection profilometry as an example, the same task can be achieved by different neural networks models with different strategies: The fringe image can be directly mapped to the corresponding phase map via DNN1; The numerator and denominator terms of the tangent function used to calculate the phase information can also be output from the fringe image and the corresponding background image via DNN2; The numerator and denominator can be predicted directly from the fringe image using a more powerful DNN

Although the above challenges have not been fully addressed, with the further development of computer science and artificial intelligence technology, it can be expected that deep learning will play an increasingly prominent role in optical metrology in the future through the following three aspects:

(1) The application of emerging technologies (such as adversarial learning, transfer learning, automated machine learning, etc.) to the field of optical metrology can promote the wide acceptance and recognition of deep learning in the field of optical metrology.

(2) Combining Bayesian statistics with deep neural networks to estimate and quantify the uncertainty of the estimate results, based on which it is possible to evaluate when neural networks produce unreliable predictions. This gives researchers another possible choice between "blind trust" and "blanket negation", namely "selective" adoption.

(3) The synergy between prior knowledge of image generation and physical models and data-driven models learned from experimental data can bring more expertise in optical metrology into deep learning frameworks, providing more efficient and "physically sound" solutions to specific optical metrology problems [Figure 22].

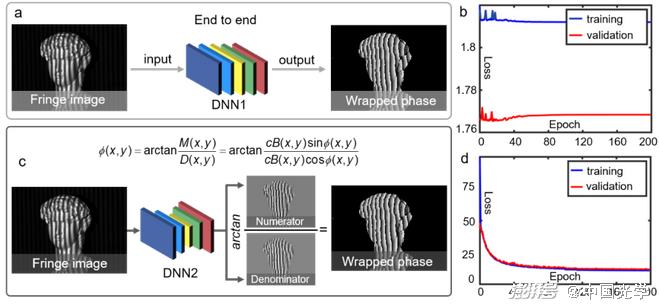
Figure 22 Introducing a physical model into deep learning can provide a more "reasonable" solution to a specific optical metrology problem. A) Directly predict the wrapped phase from the fringe image based on the end-to-end network structure (DNN1) b) It is difficult for the end-to-end strategy to accurately reproduce the 2π phase truncation, resulting in the loss function of the network not converging during training c) Incorporate the physical model of the traditional phase shift method into deep learning to predict the molecular and denominator terms of the tangent function used to calculate the phase information from the fringe image 39 d) The loss function of the deep learning network combined with the physical model can be stably converged during training

Summary and Outlook

There is no doubt that deep learning technology offers powerful and promising new solutions to many challenging problems in the field of optical metrology, and promotes the transformation of optical metrology from "physics and knowledge-based modeling" to "data-driven learning" paradigm. A large number of published literature results show that methods based on deep learning for specific problems can provide better performance than traditional knowledge-based or physical model methods, especially for many optical metrology tasks where physical models are complex and the amount of information available is limited.

But it has to be admitted that deep learning technology is still in the early stage of development in the field of optical measurement. A considerable number of researchers in this field are rigorous and rational. They are skeptical of the "black box" deep learning solutions that lack explainability at this stage, and are hesitant to see their applications in industrial testing and biomedicine. Should we accept deep learning as our "killer" solution to the problem, or reject such a "black box" solution? This is a highly controversial issue in the current optical metrology community.

From a positive perspective, the emergence of deep learning has brought new "vitality" to the "traditional" field of optical metrology. Its "comprehensive penetration" in the field of optical metrology also shows us the possibility of artificial intelligence technology bringing huge changes to the field of optical metrology. On the contrary, we should not overestimate the power of deep learning and regard it as a "master key" to solve every challenge encountered in the future development of optical metrology. In practice, we should rationally evaluate whether the large amount of data resources, computing resources, and time costs required to use deep learning for specific tasks are worth it. Especially for many applications that are not so "rigorous", when traditional physical model-based and "active policy" techniques can achieve better results with lower complexity and higher interpretability, we have the courage to say "no" to deep learning!

Will deep learning take over the role of traditional technology in optical metrology and play a disruptive role in the next few years? Obviously, no one can predict the future, but we can participate in it. Whether you are a "veteran" in the field of optical metrology who loves traditional technology, or a "newbie" who has not been involved in the field for a long time, we encourage you to take this "ride" – go and try deep learning boldly! Because it is really simple and often works!

Note: This article comes with a deep learning sample program for single-frame fringe analysis (Supplemental Material File #1) and its detailed step guide (Supplementary Information) to facilitate readers’ learning and understanding. For more details related to this article, please click　https://www.nature.com/articles/s41377-022-00714-x　Come and read the body of the 54-page paper.

Paper information

Zuo, C., Qian, J., Feng, S. et al. Deep learning in optical metrology: a review. Light Sci Appl 11, 39 (2022).　

https://doi.org/10.1038/s41377-022-00714-x

The first author of this article is Professor Zuo Chao of Nanjing University of Science and Technology, and PhD student Qian Jiaming of Nanjing University of Science and Technology is co-author. Co-authors include Associate Professor Feng Shijie of Nanjing University of Science and Technology, PhD student Yin Wei of Nanjing University of Science and Technology, PhD student Li Yixuan of Nanjing University of Science and Technology, PhD student Fan Pengfei of Queen Mary University of London, UK, Associate Professor Han Jing of Nanjing University of Science and Technology, Professor Qian Kemao of Nanyang University of Technology in Singapore, and Professor Chen Qian of Nanjing University of Science and Technology.

references

1. G?svik, K.J. Optical metrology. (John Wiley & Sons, 2003).

2. Creath, K. V phase-measurement interferometry techniques. In Progress in optics vol. 26 349 – 393 (Elsevier, 1988).

3. Aben, H. & Guillemet, C. Integrated photoelasticity in Photoelasticity of Glass 86 – 101 (Springer, 1993).

4. Gabor, D. A new microscopic principle. Nature 161, 777 – 778 (1948).

5. Schnars, U., Falldorf, C., Watson, J. & Jüptner, W. Digital holography in Digital Holography and Wavefront Sensing 39 – 68 (Springer, 2015).

6. Gorthi, S. S. & Rastogi, P. Fringe projection techniques: whence we are? Opts. Lasers Eng. 48, 133 – 140 (2010).

7. Pan, B., Qian, K., Xie, H. & Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review. Meas. Sci. Technol. 20, 062001 (2009).

8. Marr, D. & Poggio, T. A computational theory of human stereo vision. Proc. R. Soc. Lond. B Biol. Sci. 204, 301 – 328 (1979).

9. Pitas, I. Digital image processing algorithms and applications. (John Wiley & Sons, 2000).

10. Trusiak, M., Patorski, K. & Wielgi, M. Adaptive enhancement of optical fringe patterns by selective reconstruction using FABEMD algorithm and Hilbert spiral transform. Opts. Express 20, 23463 – 23479 (2012).

11. Awatsuji, Y. et al. Single-shot phase-shifting color digital holography. In LEOS 2007-IEEE Lasers and Electro-Optics Society Annual Meeting Conference Proceedings 84 – 85 (IEEE, 2007).

12. Fusiello, A., Trucco, E. & Verri, A. A compact algorithm for rectification of stereo pairs. Mach. Vis. Appl. 12, 16 ? 22 (2000).

13. Zuo, C. et al. Phase shifting algorithms for fringe projection profilometry: A review. Opts. Lasers Eng. 109, 23 – 59 (2018).

14. Zuo, C., Huang, L., Zhang, M., Chen, Q. & Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 85, 84 -103 (2016).

15. Konolige, K. Small vision systems: Hardware and implementation. in Robotics research 203 – 212 (Springer, 1998).

16. Hong, C.K., Ryu, H.S. & Lim, H.C. Least-squares fittings of the phase map obtained in phase-shifting electronic speckle pattern interferometry. Opt. Lett. 20, 931 -933 (1995).

17. Zuo, C., Chen, Q., Qu, W. & Asundi, A. Phase aberration compensation in digital holographic microscopy based on principal component analysis. Opt. Lett. 38, 1724 – 1726 (2013).

18. Langehanenberg, P., Kemper, B., Dirksen, D. & Von Bally, G. Autofocusing in digital holographic phase contrast microscopy on pure phase objects for live cell imaging. Appl. Opt. 47, D176 – D182 (2008).

19.Wang, Y. & Zhang, S. Optimal fringe angle selection for digital fringe projection technique. Appl. Opt. 52, 7094 – 7098 (2013).

20. McCulloch, W. S. & Pitts, W. A logical calculus of the ideas imperceptible in nervous activity. Bull. Math. Biophys. 5, 115 – 133 (1943).

21. Rosenblatt, F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386 (1958).

22. Rumelhart, D.E., Hinton, G.E. & Williams, R.J. Learning representations by back-propagating errors. nature 323, 533 – 536 (1986).

23. LeCun, Y. et al. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1, 541 – 551 (1989).

24. Hinton, G.E., Osindero, S. & Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 18, 1527 – 1554 (2006).

25. Krizhevsky, A., Sutskever, I. & Hinton, G. E. ImageNet classification with deep convolutional neural networks. Commun. ACM 60, 84 -90 (2017).

26. Nair, V. & Hinton, G.E. Rectified linear units improve restricted boltzmann machines.in ICML (2010).

27. Hinton, G.E., Srivastava, N., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. ArXiv Prepr. ArXiv12070580 (2012).

28. Chen, J.X. The evolution of computing: AlphaGo. Comput. Sci. Eng. 18, 4 ? 7 (2016).

29. LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436 – 444 (2015).

30. Ouyang, W. et al. DeepID-Net: Object detection with deformable parts based convolutional neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1320 – 1334 (2016).

31. Doulamis, N. & Voulodimos, A. FAST-MDL: Fast Adaptive Supervised Training of multi-layered deep learning models for consistent object tracking and classification. in 2016 IEEE International Conference on Imaging Systems and Techniques (IST) 318-323 (IEEE, 2016).

32. Dong, C., Loy, C.C., He, K. & Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 38, 295 – 307 (2015).

33. Long, J., Shelhamer, E. & Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition 3431 – 3440 (2015).

34. Ronneberger, O., Fischer, P. & Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention 234 – 241 (Springer, 2015).

35. Yan, K. et al. Fringe pattern denoising based on deep learning. Op. Commun. 437, 148 – 152 (2019).

36. Shi, J., Zhu, X., Wang, H., Song, L. & Guo, Q. Label enhanced and patch based deep learning for phase retrieval from single frame fringe pattern in fringe projection 3D measurement. Opt. Express 27, 28929 (2019).

37. Kemao, Q. Windowed Fourier transform for fringe pattern analysis. Appl. Opt. 43, 2695 – 2702 (2004).

38. Takeda, M., Ina, H. & Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. JosA 72, 156 – 160 (1982).

39. Feng, S. et al. Fringe pattern analysis using deep learning. Adv. Photonics 1, 025001 (2019).

40. Feng, S., Zuo, C., Yin, W., Gu, G. & Chen, Q. Micro deep learning profilometry for high-speed 3D surface imaging. Opts. Lasers Eng. 121, 416 – 427 (2019).

41. Qian, J. et al. Deep-learning-enabled geometric constraints and phase unwrapping for single-shot absolute 3D shape measurement. APL Photonics 5, 046105 (2020).

42. Tao, T. et al. Real-time 3-D shape measurement with composite phase-shifting fringes and multi-view systems. Opt. Express 24, 20253 (2016).

43. An, Y., Hyun, J.-S. & Zhang, S. Pixel-wise absolute phase unwrapping using geometric constraints of structured light systems. Opt. Express 24, 18445 – 18459 (2016).

44. Tao, T. et al. High-speed real-time 3D shape measurement based on adaptive depth constraints. Opt. Express 26, 22440 (2018).

45. Z’bontar, J. & LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. 32.

46. Mei, X. et al. On building an accurate stereo matching system on graphics hardware. In 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops) 467 – 474 (IEEE, 2011).

47. Pang, J., Sun, W., Ren, J. SJ., Yang, C. & Yan, Q. Cascade Residual Learning: A Two-Stage Convolutional Neural Network for Stereo Matching. in 2017 IEEE International Conference on Computer Vision Workshops (ICCVW) 878 – 886 (IEEE, 2017). do i: 10.1109/ICCVW.2017.108.

48. Montresor, S., Tahon, M., Laurent, A. & Picart, P. Computational de-noising based on deep learning for phase data in digital holographic interferometry. APL Photonics 5, 030802 (2020).

49.Li, Z., Shi, Y., Wang, C., Qin, D. & Huang, K. Complex object 3D measurement based on phase-shifting and a neural network. Opt. Commun. 282, 2699 – 2706 (2009).

50.Li, Z., Shi, Y., Wang, C. & Wang, Y. Accurate calibration method for a structured lighting system. Opt. Eng. 47, 053604 (2008).

51. Feng, S., Zuo, C., Hu, Y., Li, Y. & Chen, Q. Deep-learning-based fringe-pattern analysis with uncertainty estimation. Optica 8, 1507 – 1510 (2021).

Article reprint/business cooperation/research group submission, WeChat:447882024

Let’s read one article a day!Join >Light reading club

Original title: The 100 most beautiful friends in winter, for you.

Click on the picture,studySpring and Autumn Chinese Painting Course!

In all kinds of seasons with the deepest feelings about winter,

There must also be appropriate words to match them!

How about from the following 100 sentences about winter,

Pick out your exclusive winter friend circle copy!

Image from @ Palace Museum

one

Start like spring, continue like summer,Turn into autumn and close into winter. (Feng Jicai)

2

No matter how cold, windy and snowy,Thinking of these, my heart is always warm. (Zhu Ziqing)

three

Winter is solemn and quiet, which makes everyone meditate.Instead of being frivolous. (Jia Pingwa)

four

It turns out that winter rhyme is related to people’s mood.Open your heart, release your mood, and winter is rhyme. (Gan Zhen)

five

The stream firewood is soft and warm,I don’t go out with raccoon slaves. (land tour)

six

Freezing pen and writing new poems are lazy,A cold stove and a good wine are warm. (Li Bai)

seven

The inkstone ice is old in snuff,I still hold my robe for books. (wentong)

eight

The more cold winter is, the fate of winter is coming to an end, and "spring" is already knocking at the door. (Mao Dun)

nine

Life also has winter and summer, childhood is like summer, and adulthood is like winter; Or young as summer, eldest as winter. (Feng Zikai)

10

Although people know that there will be strong winds, snow and ice, it does not reduce the interest; On the contrary, everyone hopes and prepares to enjoy the gossip around the stove in winter, chewing sweet and crisp radish or Sugar-Coated Berry. (Lao She)

11

Whether you like it or not, you must go out into the street to welcome the arrival of winter. (Su Tong)

12

I can only write letters in the snow and write down everything you want to know. Come on, before it’s too late, the letter will melt.(Gu Cheng)

13

There are thousands of books on hakodate, and a ladle of wine is spent. (Xu Hun)

14

Koharu will not be here for many days, and plum blossoms will bloom. (Chou Yuan)

15

I heard that the plum blossoms have blossomed three or two, and I am waiting for you with a seat of tea. (Xue Xiaochan)

16

The sky is dark and smoky, and the famous papers are handed down to celebrate the winter. (Ma Zhen)

17

Day and personnel, every day changes quickly, and then to the winter solstice, after the winter solstice, the day after the warmer, the spring is coming back. (Du Fu)

18

If you don’t feel much for the mountains and rivers, you will be fascinated by the poor wanderer. (land tour)

19

Snow is a big romance, and you are a little person. (anonymous)

20

Every winter, we can really touch the years. (Feng Jicai)

21

If you don’t come, it’s going to snow. (Muxin)

22

I made a snowman in front of your door/on behalf of clumsy me/keeping you waiting. (Gu Cheng)

23

Keep warm with your name. Snow, have big. (Haisang)

24

Keeping the world quiet for a while is one of Xue’s missions. (Yang Limin)

25

A pinch of snow. Souvenirs of the long winter. (Abbas)

26

You can treat me with snow with confidence. (paul celan)

27

As the wind changes, the snow changes. I can’t dream of breaking my hometown, so there is no such sound in my hometown. (Nalan Xingde)

28

We cannot see all the snow that falls in a person’s life. Everyone spends the winter alone in his own life. (Liu Liangcheng)

29

Chai Men smells dogs barking, and the snow returns home at night. (Liu Changqing)

30

Although the mountain road is far away, but I will not refuse your kind invitation; Even if the heavy snow thick, also to visit the snow, and now is the spring, the ice has melted. (Zhang Jiuling)

31

As usual, it is different to have plum blossoms before the window and the moon. (Du Lei)

32

In winter, in the snow, ups and downs, can eat a cup of black tea, I think, is blessed. (Plantago asiatica)

33

With dusk, the snow is impending, what about a cup of wine ? (Bai Juyi)

34

The snow in the south of the Yangtze River and the north of the Yangtze River is long. (Xiang Ziyin)

35

The Miyagi Regiment returned to Yan Guang, where it was smashed into Qiong Fang during the day. (Li He)

36

Arouse a bright moon, shine on me full of ice and snow, and the mighty rivers flow. (Xin Qiji)

37

What is life like everywhere? It should be like flying through the snow. (Su Shi)

38

Fingers are sticking out of the window through the glass/a snowflake has just been measured/the temperature of the Alps/it beats slightly in my palm. (Shu Ting)

39

It’s snowing heavily. In such a deep night, snowflakes should cover the footprints of lovers, the steps they have sat on, the grass they passed by and the tears they left in a street. (Zhang Jiajia)

40

It has just snowed here/it seems that all human love falls to a low place/you sit under the window/the window is suddenly hit by the sun/what a crisp sunshine/it seems like a rare joy in your life. (Huang Lihai)

41

May you have shelter from the wind and rain and a stove to warm you, but most importantly, I wish you love when the snow is falling. (john crowley)

forty-two

In-between the colors of Moon and Snow, You would be the third color rivaled by none. (Yu Guangzhong)

43

There are flowers in spring, moons in autumn, cool breeze in summer and snow in winter. If you don’t mind your own business, it is a good time on earth. (Master Hui Kai)

forty-four

If your eyes are really so cold, there is someone under your eyes.The heart will turn into ice. (Shen Congwen)

45

If you want to sit at home late at night, you should also talk about travelers. (Bai Juyi)

46

Three feet of snow in front of the door makes you gasp. (Zhao Bingwen)

47

I love to sit around the warm fire on winter nights, chat with two or three former friends, and listen to the north wind rustling the doors and windows, while we recall the happy and carefree past years. (Mu Dan)

48

Around the stove, at night.

Meet in an old family,

A small fire is warm, and tea smoke is floating.

Have a long talk, have a clear talk on a cold night,

Look at the faint sinking of the moon, listen to the rustling of snow and falling tiles.

Life comes and goes sometimes, no matter how late at night.

(anonymous)

forty-nine

I am an old acquaintance of Yu and Xue. I am ninety years old. Rain and snow have aged me, and I have aged them. (Chi Zijian)

50

A pinch of snow. Souvenirs of the long winter. (Abbas)

51

Walking and walking, it began to snow. The snow was fine and I was fine. It knocked on your window and I knocked on your door. (Haisang)

fifty-two

The light snow falls on the old eaves, the new stove is hot and aging, and the moon sets on the hills, so the old man angelica sinensis. (anonymous)

53

The earth will not age, and winter is just a quiet dream; It will wake up in the warm spring breeze and make itself young again. (Lu Yao)

54

It should be the immortals who are drunk and crush the white clouds. (Li Bai)

55

I left a lamp. On a snowy night in the city, as long as you come with wine, don’t say Qian Shan, don’t say brief encounter. (anonymous)

fifty-six

Haizi said: When you come face to face, the ice melts and the snow melts. I said: hold your hand and warm the winter together. (anonymous)

57

The family is sitting around, and the lights are amiable. (Wang Zengqi)

58

I often go to bed early in cold weather, not waiting for the sun to gather. (Shi Wenjun)

59

The lotus is old when it is defeated, and the cold light is dim and the grass is fading. (Zhao Changqing)

60

It snows in my world. (Chi Zijian)

61

I want to bring a handful of snow in the cold winter, store it in the next year, and wash your vicissitudes of life. (anonymous)

62

The sky and the clouds and the mountains and the water are white. (Zhang Wei)

63

Snow makes people feel young again. (Yukio Mishima)

64

You are not here, spring, summer, autumn and winter; You are here, spring flowers and autumn fruits, summer cicadas and winter snow. (anonymous)

65

Legend has it that people in the Arctic, because of the freezing weather, turn into ice and snow as soon as they speak, and the other party can’t hear them, so they have to go home and bake slowly to listen … (Lin Qingxuan)

66

If there is no snow in the world, human beings will never be able to synthesize such things out of thin air by existing imagination. (Li Juan)

67

I can only write letters in the snow and write down everything you want to know. Come on, before it’s late, the letter will melt. (Gu Cheng)

sixty-eight

The beauty of time lies in its inevitable passage: spring flowers, autumn moon, summer and winter snow. (San Mao)

sixty-nine

If you are lovelorn and can’t wait until the ice and snow melt, put a torch to burn down the igloo and burn it into another spring. (Lin Qingxuan)

70

What is life like everywhere? It should be like flying through the snow. (Su Shi)

71

Think of the quietest things, such as snow. (truman capote)

seventy-two

Fingers are sticking out of the window through the glass/a snowflake has just been measured/the temperature of the Alps/it beats slightly in my palm. (Shu Ting)

73

Arouse a bright moon, shine on me full of ice and snow, and the mighty rivers flow. (Xin Qiji)

74

If I were a snowflake, dashing in mid-air, I would definitely know my direction-flying, flying, flying,-(Xu Zhimo)

75

Snow and snow reflect each other-tonight is like the Mid-Autumn Festival in December. (Matsuo Bashō)

76

Sometimes it is not necessarily apricot blossoms and spring rains, fallen leaves and flying flowers that make a person’s enthusiasm for life, but the snow falls in Qian Shan and the ancient trees are pale. Only when there is great grief can there be great hope. (Zhu Yong)

77

I can’t help crying: "It’s really snowing …" just like I said "I really love you". (Li Juan)

seventy-eight

See a candle in the wind on a snowy night. Watch the setting sun in the evening sunset. Think of friends far away in the middle of the night when pine nuts fall. I suddenly miss my brother on the highest mountain. In a falling white hair, the favorite face of my life emerges. (Lin Qingxuan)

79

I still like walking at dusk, watching the sunset in the water, watching the fallen leaves in the wind and watching the mountains in the snow. I am not afraid of getting old, because I want the moonlight to blend with my hair when my hair turns white. (Chi Zijian)

80

Time passes through the river of the twelfth lunar month and sails to the end of the year. The year is like the snow in the winter of the earth, which is dense and deep day by day. (Feng Jicai)

81

Inexplicably, I remembered a family photo taken by relatives at home on a snowy day many years ago. (ZhuSelf-cleaning)

82

The so-called determination, we don’t choose other ways to get here, so let’s finish this map together: watch the first snow together, sweep the snow together, hibernate together, and grow old smoothly together … (Lin Wanyu)

83

It’s only in the cold that there is good snow in Fukashi.Miss the stormy wind that night,Snow bristles roared all over the sky.When I wake up in the morning, the frozen window will shine brightly. (Zhu Wei)

84

Recall that when the original expedition, yang liuyi wind blowing in the wind; Now back on the road, the snow is flying everywhere.The road was muddy and hard to walk, and the thirsty and hungry. (The Book of Songs Xiaoya)

eighty-five

The Slender hands were cold, not to mention the cold scissors to cut out the garments.(Li Bai)

86

Coody Leng’s dream is broken, and the cold wind combs his bones. (Meng Jiao)

87

The desert iced over thousand feet and there was a crack, and the sky filled with gloom and gloom. (Cen Can)

88

No bird is flying among those mountains, and no man traces can be seen among those paths. (Liu Zongyuan)

eighty-nine

It’s sad at the end of the year, and it’s snowing. (Tao Yuanming)

90

It was late at night to know that the snow was very large, because from time to time it could hear the sound of the bamboo branches folded. (Bai Juyi)

91

Snow and moon are most suitable, and Mei Xue is clear. (Zhang Xiaoxiang)

92

The cold frost on the door can wake up the bones, and the afterglow on the window is good for reading. (Zijin cream)

93

After the winter solstice, it is called, and after the summer solstice, it is inhaled. The breath of one year old in this world is also. (Huang Ji Jing Shi)

94

The existence of coldness may help you find something warmer. (@ 么么么么么 o)

95

Life should drink a feast, the best in half – drunk and half – awake. The heavy snow in Chang an all over the sky, blocking the passage of the road. (Shu Shu)

96

I’m sorry you didn’t see it, but now the snow is falling from the stars. (truman capote)

97

Everyone knows that no one is worried about me. Tonight, it snows and there are plum blossoms, which is like me. (Jie Jiang)

98

For the snowman, what happened before the hot sun appeared was a trivial matter. For life, if it is something that can be reached by walking constantly, it is a small matter. For memories, if they are forgotten, they can be put down, and they are all small things. (Lin Wanyu)

99

The time series enters the winter, just as people are getting old, slowly approaching, and the daily changes are subtle, which is extremely difficult to detect, and it will eventually become a severe winter. (Alain de Botton)

100

May you have mountains and trees to live in all your life.With the person you love, enjoy flowers in spring and enjoy the cool in summer. Climb mountains in autumn and sweep snow in winter. (@ That Colorful Xiangyun)

What is strong is the power of life, and what is weak is the interest of winter.

Hard is the cold of winter, soft is the warmth of people’s hearts.

This may be the spiritual elegance that we have regained from the winter.

The 100 most beautiful friends in winter,Give it to you-

May time slow down and old friends stay;

May you be safe in the cold and happy in Chang ‘an.

The essence of Chinese studies and the art of life gxjhshys are original, please indicate the reprint.

Note: This article comes from the Internet, and the copyright belongs to the original author. It is only for everyone to share learning and appreciation. If the author thinks it involves infringement, please contact us and we will delete it immediately after verification.

Read the original text and taste my ice and snow feelings!

Editor in charge: